Collaborators:

Sponsor:

RA:

 

Bill Gray and Casey Miller, Univ of North Carolina

NSF CDI Program

Kendra Brown

This project is part of a larger collaborative effort with colleagues from North Carolina under an NSF funded project: Collaborative Research: CDI-Type II—Revolutionary Advances in Modeling Transport Phenomena in Porous Medium Systems

The focus is the development of a first principles, multiscale theoretical and computational approach, which we refer to as the thermodynamically contrained averaging theory (TCAT) approach, that we believe will lead to a paradigm shift in the way in which multiphase porous medium systems are modeled. Through joint development of theory and use of high resolution, multiscale computation we will advance a new generation of models that resolve many of the outstanding issues in the field. Importantly, the establishment of this approach will provide a platform for the rigorous advance of models of a wide range of systems of varying complexity that will serve to support the work of others engaged in the study of porous medium systems as well. The tools of this work include continuum mechanics, thermodynamics, multiscale analysis, high resolution lattice Boltzmann simulation, and advanced integral methods for solving systems of nonlinear partial differential algebriac equations. The OSU component involves generation of 2-phase and 3-phase data sets in support of the model development.

This data and microscale simulations will be used to guide the development of two-fluid phase
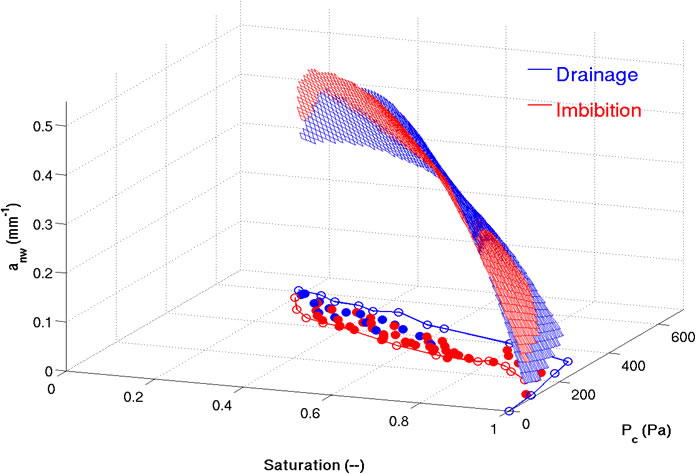
flow models and to verify the utility of the models. I nt he past, we have made detailed observations of two-fluid-phase flow systems using a synchrotron high-energy source. These observations include fluid displacement and non-wetting fluid entrapment and quantities such as the morphology and topology of the pore space, interfacial areas, and common curve lengths. Recent measurements by our group have shown that inclusion of the wetting-nonwetting interfacial area as a third variable describing the relationship between capillary pressure and saturation confirms the theory by Gray and Hassanizadeh, which suggests that hysteresis is absent from a capillary pressure-saturation-interfacial area surface Porter et al., 2010.

The third class of application that will be considered is three-fluid-phase flow and transport.
These phenomena occur in a wide variety of applications. The approach taken to model three-fluid-phase flow is similar to that described previously for two-fluid-phase flow. However, because of the higher complexity of such systems, less work has been done to characterize them, and experimentally based relationships among fluid pressures, volume fractions, and permeabilities are significantly more difficult to infer. The limitations of standard three-fluid-phase flow models are identical to those noted for the two-fluid-phase flow case, but they are amplified because of the additional interfaces and common curves that can form and impact system behavior. For example, the cornerstone of multiphase flow models is the relative permeability, accounting for the reduction in flow due to the mutual interaction of the different flowing phases. In reservoir engineering, relative permeability has been implemented with and without hysteresis. However,
a striking disparity in the simulation results for a three-phase flow problem was demonstrated depending on whether or not hysteresis is employed. Furthermore, most reservoir engineering models (and those used to simulate CO2 injection) implement relative permeability hysteresis empirically via so-called trapping models, which predict trapped residual nonwetting phase volume based on knowledge of the initial nonwetting phase saturation. In general, trapping models have all been compared to the same data set. Thus additional experimentation and improved model formulations are needed. Because one of the safer methods of permanent storage of CO2 in the subsurface is based on capillary trapping following injection, the accuracy with which such a process can be predicted using numerical models will be of crucial importance to decision-makers. Synchrotron methods and LBMs for two-fluid-phase flow will be extended to observe and model three-fluid-phase flow.