The Laboratory for Robotics and Applied Mechanics investigates fundamental mathematical principles in locomotion, manipulation, and perception.
Spider Webs
Due to their poor eyesight, orb-weaving spiders rely on web vibrations for situational awareness. Web-borne vibrations are used to determine the location of prey, predators, and potential mates. The influence of web geometry and composition on web vibrations is important for understanding spider’s behavior and ecology. We are constructing artificial webs and computer models to better understand the effect of web structure on vibration transmission.
By creating scaled-up artificial spider webs we can easily make changes to web geometry and string stiffness, as well as take direct measurements of web vibrations - all of which are quite difficult to do with the delicate orb weaver spider web. Our aim is to develop useful models for the vibration of networks of strings, validate these models using experimentation, and the extend these models into the realm of biology using the properties of spider silk and observed web geometry.
This project is a collaboration with the Elias Lab at UC Berkeley, and funded by Physics of Living Systems at the National Science Foundation.
Watch a video in which Ainur describes our work. For more information regarding the SpiderHarp, please visit the SpiderHarp website.
| Press |
|
SpiderHarp: Oregon scientists study spiders with a web-inspired musical instrument -- Oregon Public Broadcasting Giant web probes spider's sense of vibration -- BBC News Earth's weird and wonderful animal models -- National Science Foundation Highlights from the APS March Meeting 2016 -- American Physical Society |
Geometric Mechanics and Undulatory Locomotion
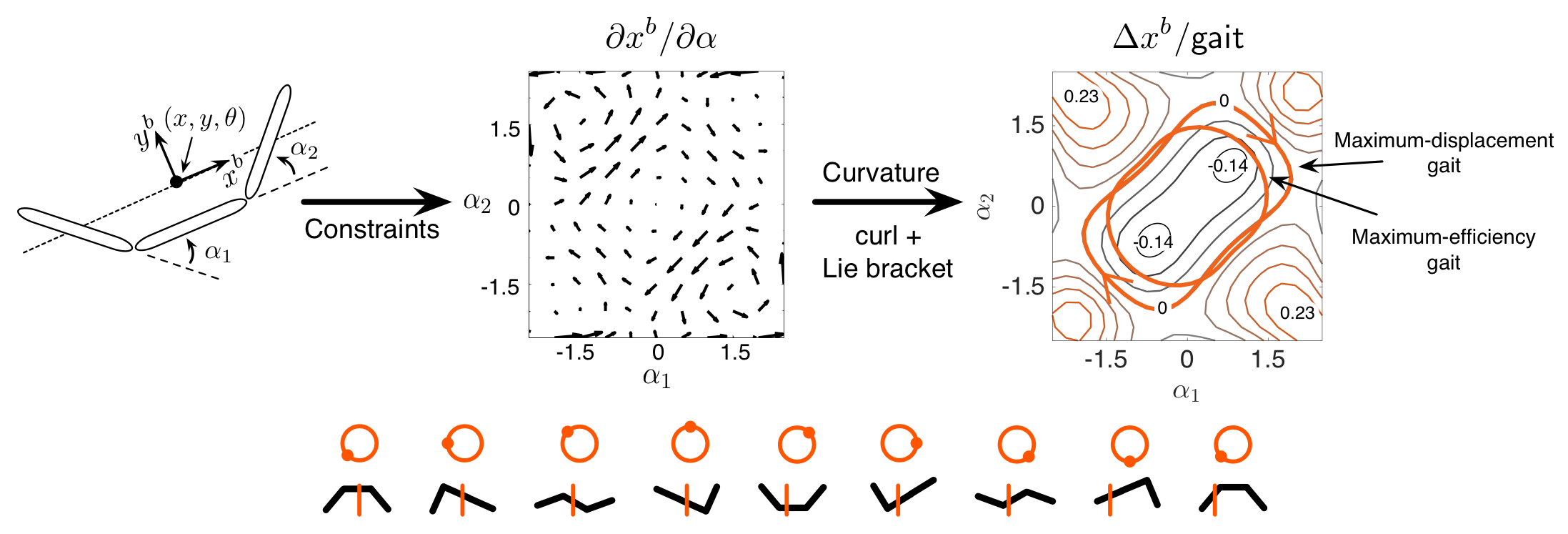
Many locomoting systems employ gaits – cyclic changes in shape – to move through the world. A fundamental principle of gait-based locomotion is that the system needs some way of changing its dynamics across the cycle in order to be able to extract net displacement. For example, the three-link system below is able to translate forward while executing a gait because the curvature of its constraints is non-zero. Its maximum-displacement gait (analogous to the longest stride a walker can take) follows the zero-contour of the curvature, enclosing a sign-definite region. Its most efficient gait (analogous to a comfortable stride) is a contraction of this curve, enclosing only the high-value portion of the curvature at the center.
An ongoing theme of our research is to generalize these principles to broader classes of systems and make the underlying mathematics tractable to researchers who do not have a background in pure mathematics.
Our Geometric System Plotter tool can be found by clicking this link.
This research is supported in part by Dynamics, Controls, and System Diagnostics at the National Science Foundation, through both regular and CAREER grants.
| Publications: |
|
Tethered Systems
 Casting manipulation is the act of launching a tethered projectile and controlling its ballistic trajectory through tension applied through the tether. In particular, we focus on manipulations that involve the interaction of tether and/or projectile with a remote target, such as wrapping a target with the tether.
Casting manipulation is the act of launching a tethered projectile and controlling its ballistic trajectory through tension applied through the tether. In particular, we focus on manipulations that involve the interaction of tether and/or projectile with a remote target, such as wrapping a target with the tether.
This line of research also includes an investigation of tether-aided locomotion, using jumping spiders and spiders dangling from draglines as inspiration and model systems.
This research is supported in part by DARPA's Robotics Fast Track program.
| Publications |
|