Parrish Research Group

Christopher Parrish (2020)

The following empirical equation can be used to compute the index of refraction of saltwater or freshwater to 3-4 decimal places:

n = aT² + bλ² + cT + dλ + e

n = index of refraction

T = temperature in deg C (valid range: 0-30)

λ = wavelength in nm (valid range: 400-700 = visible spectrum) 

Coefficient	Seawater (S = 35‰)	Freshwater (S = 0)
a	-1.50156×10-6	-1.97812×10-6
b	1.07085×10-7	1.03223×10-7
c	-4.27594×10-5	-8.58125×10-6
d	-1.60476×10-4	-1.54834×10-4
e	1.39807	1.38919

Background

While the internet might tell you that the refractive index of water is 1.33, it is actually a function of the wavelength of the light, as well as the salinity, temperature, and pressure of the water. If you are working with bathymetric lidar (λ = 532 nm, usually) or mapping bathymetry using structure from motion (SfM) photogrammetry, you almost certainly don’t want to just use this generic, approximate value of 1.33. (If you're working in seawater and just need an approximate value for the visible spectrum, 1.34 is a better approximation than 1.33.) I developed the equation and coefficients above by reading tabulated values of the index of refraction from Mobley (2010) into MATLAB and doing surface fitting. The tabulated values are for atmospheric pressure. The R² values of my surface fits were 0.998, with the RMSEs being on the order of 2×10^-4 for both seawater and freshwater. MATLAB surface plots are shown below:

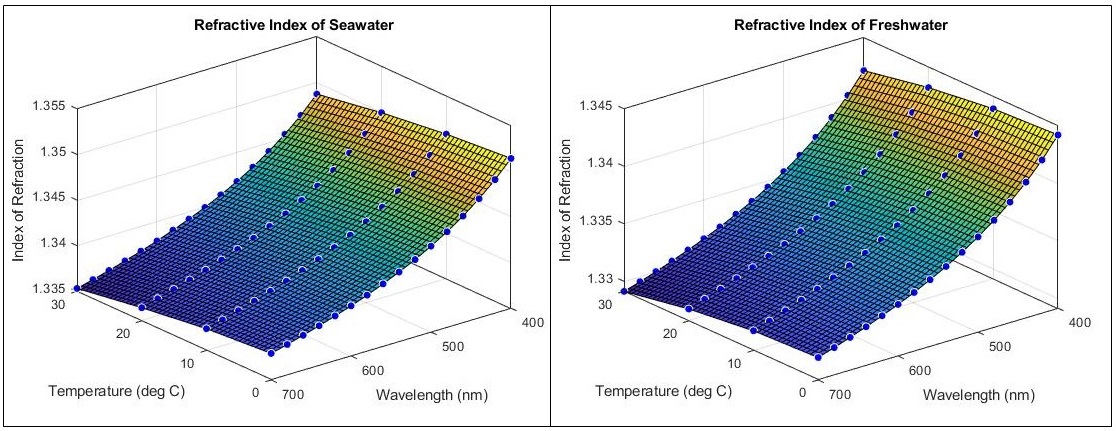
The tabulated values used as input to this process are from Mobley (2010), which, in turn, are based on Austin and Halikas (1976), which, in turn, included data compiled from a variety of sources (all referenced therein). For anyone who wants to delve further into the index of refraction of seawater as a function of salinity, temperature, and pressure, the Austin and Halikis paper is an excellent reference. There are likely newer and more accurate data than used in this 1976 study, but I haven’t found a clearer or more informative treatment of the subject. Note that greater precision in the value of n can be obtained by interpolating the tabulated values in Austin and Halikis (1976) than by using the equation above.

MATLAB code is available on this GitHub repo

What if you need to compute the refractive index for a salinity other than 0 or 35‰? According to Austin and Halikas (1976), which contained data used to generate the tables in Mobley (2010), which in turn, were my starting point for deriving the equations above: “dependence of index on salinity is linear for all combinations of the other three parameters.” So, for estimating the refractive index for salinities other than 0 or 35‰, it should be possible to linearly interpolate. For example, if n = 1.3347 for S = 0, and n = 1.3411 for S = 35‰ (for the same wavelength and water temperature), and you want to find the refractive index for S = 30‰, you could compute it as: n = (1.3347(35-30) + 1.3411(30))/35 = 1.3402.

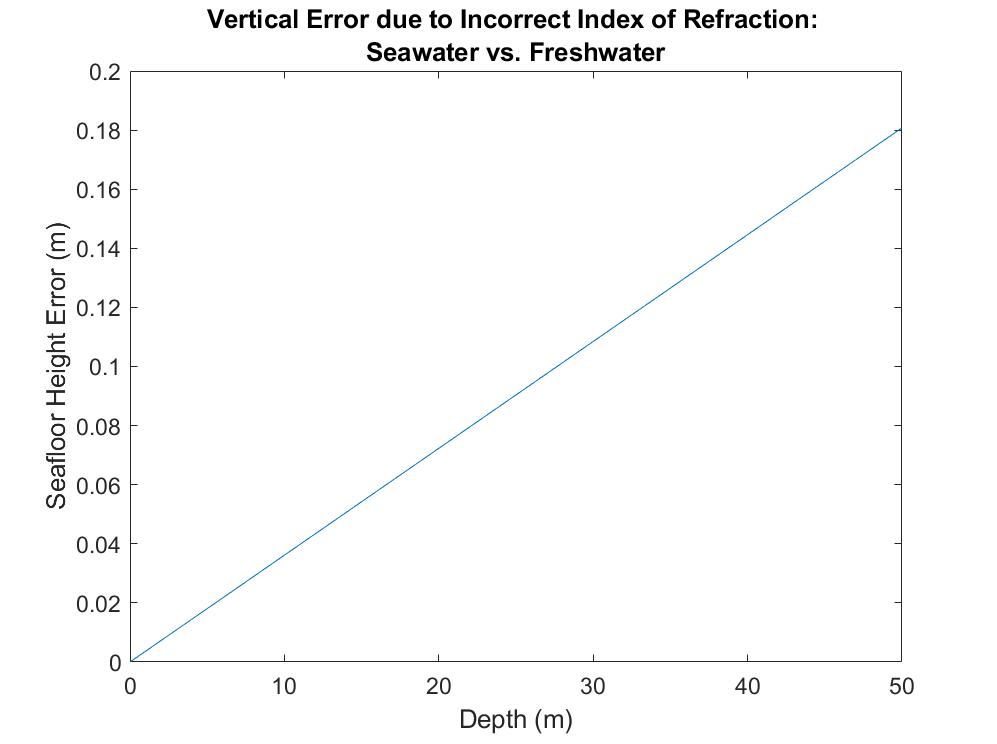
So, how much of a difference does the index of refraction actually make in bathymetric lidar? The answer is that it can make a big difference, especially, if you use a freshwater index, when working in seawater or vise versa. Below is a plot of the vertical error in refraction-corrected bathymetric lidar points due to using a freshwater vs. seawater index of refraction as a function of depth. At 50 m water depth, the error in the computed seafloor height is over 18 cm. (Please note that this analysis is not a propagation of random uncertainties, but, rather, an assessment of the impact of a large systematic error, which could even be characterized as a blunder--namely, using a freshwater index of refraction, when a seawater index of refraction should instead be used.)

 

 

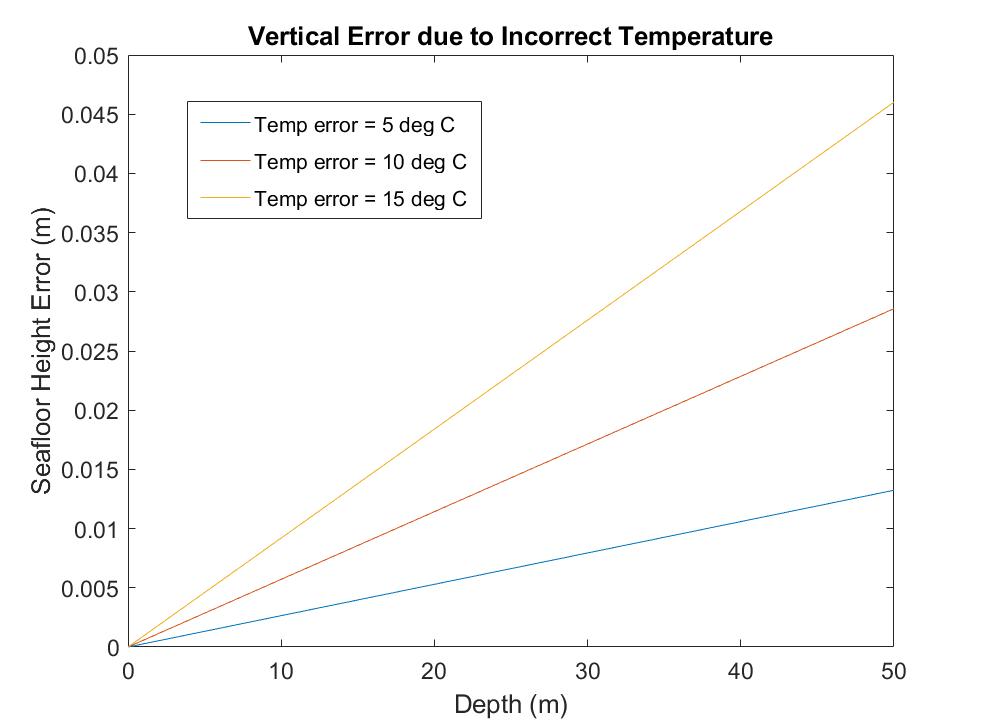
Recently, some colleagues asked me how much of an impact water temperature has on bathymetric lidar refraction correction. Or, if there's a systematic error in the water temperature used in calculating the index of refraction, how large will the resultant error in refraction-corrected seafloor heights be? To answer this, I assumed the following “true” values: S = 35‰, λ = 532 nm, and T = 15.0 °C. Then, I assumed temperature errors (again, systematic errors or biases--not random uncertainties) of 5.0 °C, 10 °C, and 15 °C and plotted the resultant errors (absolute value) in refraction-corrected seafloor heights for water depths of 0-50 m. Below are the results. My interpretation is that, as long as you don't have a large systematic error in temperature, the resulting error in the computed seafloor height should not be too bad at most depths. But, with larger temperature errors and at greater depths, the errors will again be too large to be ignored. As is always the case, the better job you can do at removing systematic errors, the better your final data will be.  

 

I recently updated this analysis, using more formal uncertainty propagation procedures. More specifically, I used the special law of propagation of variances (SLOPOV) to investigate how uncertainty in the index of refraction of water propagates to uncertainty in the computed seafloor height in bathymetric lidar. A first-order bathymetric lidar refraction correction (accounting only for vertical correction, not planimetric) is (Parrish et al., 2019):

where Z_c is the depth correction (i.e., the vertical distance by which the uncorrected depth gets shifted up in the refraction correction procedure), n_a is the refractive index of air, n_w is the refractive index of water, and D is the uncorrected depth. Differentiating with respect to n_w gives:

From SLOPOV:

Next, we can plug in some numbers. Say depth, D = 30 m, n_a = 1.00029, n_w = 1.3425, and   = ± 0.009 (uncertainty in the index of refraction of water, unitless). (Admittedly, this would be a fairly large uncertainty.)

 

Multiplying by 1.96 to convert to a 95% confidence level (which assumes a Gaussian distribution), we get ±0.29 m

So, 29 cm of uncertainty in 30 m of water. Is this acceptable? To answer this, we refer to the International Hydrographic Organization IHO S-44 standards, and see that for Special Order hydrographic surveys, the maximum permissible total vertical uncertainty (TVU), at the 95% confidence level is:

Bottom line: in this case, the uncertainty in the index of refraction alone (not even considering other component uncertainties) would nearly, but not quite, cause us to not meet survey specs. 

For more information on how these values are used in research, please visit my research group's website.

 

References

Austin, R.W., and G. Halikas, 1976. The Index of Refraction of Seawater. SIO Ref. No. 76-1, Scripps Institution of Oceanography. San Diego, California.

Mobley, C.D. 2010. The optical properties of water. In Handbook of Optics (Eds. M. Bass), 3rd edition. McGraw-Hill, New York, Vol. 4, pp. 1.3–1.53.

Parrish, C.E., L.A. Magruder, A.L. Neuenschwander, N. Forfinski-Sarkozi, M. Alonzo, and M. Jasinski, 2019. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sensing, Vol. 11, No. 4: 1634.